Do not short any battery box or power
supply.
Use the component holder to connect the
small electronic components.
Set R at maximum before connecting the
Potentiometer, Rheostat, Resistance Box in the circuit.
Turn off the multimeter by setting the
selector in any range but NOT in Ohm-Scale after used.
Do not change the range of the multimeter
when it is being connected.
Do not touch any optical part ( e.g. the
grating, the slit slide, & the lens etc.) of the
optical instrument.
Be careful and don't make any scratch on
the optical instrument. Remember to pack it up after use.
Do not strike the pins on the wooden
board. Fix the pins by pressing it with your finger only.
Set the amplitude of the signal generator
at zero output before switching
it on/off.
Let the CRO on all the
time until the end of the experiment. (When it is not in
use temporary, just turn down its intensity.
Turn the amplitude of Signal Generator to
zero when not in use.
Check the amplitude of Signal Generator
setting at zero position whenever you turn on
or off the signal generator.
A measurement can never be assumed to be one hundred percent
correct. No matter how careful it is taken, there is always some
uncertainty about it. An error is a measure of the
degree of uncertainty of a measurement. It is not to be
confused with a mistake which arises from the use of an incorrect
method or procedure.
Errors in a particular experiment may be due to the
limitations of the experimenter, the measuring instrument, or the
method used. Experimental- errors are basically of two types:
system and random.
It is important to be able to estimate the possible error in a
measurement. Here we are mainly concerned with estimation of the maximum
possible error and a simple case of random error.
A measurement quoted as 4.82 m implies that it lies somewhere
between 4.815 m and 4.825 m. It is said to be given to 3
significant figures. A length measured as 4.8 m to 2 significant
figures is less accurate and is taken to lie somewhere between
4.75 m and 4.85 mm. The number of significant figures to which a
measurement is given implicitly indicates a certain order of
accuracy.
The result of an experiment is usually calculated from an
expression which contains a number of physical quantities that
have been measured. The error in the result can be worked out
from the errors in the various measurements. The following shows
how this is done for some simple cases.
- Sum and difference
Two temperature readings are
recorded, using a thermometer reading to the nearest 0.2oC,
as (10.5 +0.2)oC
and (21.3 + 0.2)oC.
Percentage errors in the two readings are about 2% and 1%
respectively.
When the two temperatures are added together, the
result is (31.8 + 0.4)oC,
which has an error of about 1%. When the two temperatures
are subtracted, the errors in the two readings are added
up, rather than sub- tracted from one another, since we
are estimating the maximum possible error that may arise.
Of course the two errors may cancel each other out, but
we cannot take this for granted. The result is thus (10.8
+ 0.4)oC which has
an error of about 4%.
- The square or cube of a measurement
The radius
r of a wire is measured as (0.52 + 0.01) mm, with
an error of 1.9%. Cross-sectional area A of the wire is
calculated by the formula:
A= pr2
= p(0.52)2
mm2 =
0.850 mm2
Therefore lies between p(0.53)2 mm2
and p(0.51)2mm
2 , i.e.,
between 0.882 mm2
and 0.817 mm2.
Hence we can write A as (0.850 + 0.033) mm2.
The error in A is 3.8% which is twice in r . This can,
infact, be shown, using calculus as follows:
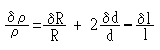
Each term on the right side, when multiplied by 100,
represents the percentage errors in R, d and l and
hence the percentage error in r
can easily be found. Since we consider maximum possible
errors, the percentage error in l has to be added to,
rather than subtracted from, the sum of percentage errors in
R and d.
Hence 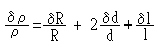
Example
In determining the resistivity of a metal wire, the
following measurements are made:
Resistance R of wire = 6.7 + 0.1 W (1.5 % error)
Diameter d of wire = 0.51 + 0.01 mm (2 % error)
Length l of wire = 2.56 + 0.01 m (0.4%)
Resistivity of the metal wire
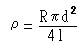 =5.35 x 10 -7 Wm
=5.35 x 10 -7 Wm
% error in r
=% error in R + 2 x %error in d + %error in l
=(1.5 + 4 + 0.4 ) %
=5.9 %
5.9% of 5.4 x 10-7
W m is 0.32 x 10-7 W
m.
As the error is 5.9%, it is obviously incorrect to give
the result for r to 3 significant
figures, since this implies an order of accuracy of 0.1%. The
result should thus be given to 2 significant figures only, as
r = (5.4 + 0.3) X 10-7 W m
Improving the accuracy
In the above example, the length of the wire was measured
to the nearest cm and this gives an error of 0.4%. Measdring
the length to the nearest mm gives a much smaller percentrage
error, 0.04%, but this would be pointless since this has to
be added to the much larger percentage errors in R and d2. In doing any
experiment, we should have some idea of the order of accuracy
among the different quantities measured. We should
concentrate our effort on trying to reduce the error of the
readings which are most uncertain, instead of wasting time in
improving the accuracy of those readings which are already
quite accurate by comparison.
How could the accuracy of the resistivity in the example
be improved? The diameter of the wire has the largest
percentage error, but it is not easy to find . more accurate
instrument than the micrometer screw gauge which measure to
the nearest 0.01 mm. Using a greater length would help, since
this increases the resistance value R and so reduces the
percentage error in R (assuming the accuracy of the
Wheatstone bridge for measuring R is unchanged).
Graphs
Most experiments in physics require the drawing of graphs.
Apart from providing an immediate visual picture of results
and information, a graph can
(a) show how one variable quantity is related to another;
(b) be used to determine the constants in an equation
relating two variable quantities;
(C) provide the best way of 'averaging' a set of readings.
These functions will be explained in detail later.
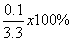 or about 3%.
or about 3%. 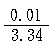 x
100% or 0.3%. The reading error of an instrument depends
on the accuracy with which it is calibrated.
x
100% or 0.3%. The reading error of an instrument depends
on the accuracy with which it is calibrated.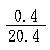 by moving the
screen until the image is just blurred. Thus an
image distance may be recorded as (20.4 + 0.4) cm
if the image on the screen is just out of focus at 20.0
cm and also at 20.8 cm. This gives a percentage error of
x 100% or 2%.
by moving the
screen until the image is just blurred. Thus an
image distance may be recorded as (20.4 + 0.4) cm
if the image on the screen is just out of focus at 20.0
cm and also at 20.8 cm. This gives a percentage error of
x 100% or 2%.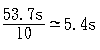
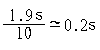
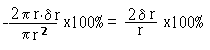
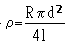
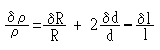
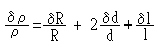
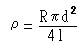 =5.35 x 10 -7 Wm
=5.35 x 10 -7 Wm